奇異值分解（Singular Value Decomposition, SVD）筆記

Last Updated on 2024-08-11 by Clay

奇異值分解（Singular Value Decomposition, SVD）是一種將矩陣分解為三個矩陣乘機的方法，揭示了原矩陣的秩（Rank）、資料維度及重要方向，經常用於降維、壓縮和結構分析。

設 A 為一個 m x n 的矩陣，SVD 可以寫為：

$\displaystyle A = U \Sigma V^T$

其中 $\displaystyle U$ 為 $\displaystyle m \times m$ 的形狀、 $\displaystyle \Sigma$ 為 $\displaystyle m \times n$ 的形狀、 $\displaystyle V^T$ 為 $\displaystyle n \times n$ 的形狀，且：

$\displaystyle U$ 為實正交矩陣，亦即 $\displaystyle U^T=U^{-1}$ ，是 A 的左奇異矩陣
$\displaystyle V$ 為實正交矩陣，亦即 $\displaystyle V^T=V^{-1}$ ，是 A 的右奇異矩陣
$\displaystyle \Sigma$ 為類對角矩陣（因為其並不一定為方陣），只有對角元素可能有非零的數值，其餘元素皆為零；其對角線上的元素是 $\displaystyle A$ 的奇異值。

其中，上圖的 $\displaystyle r$ 代表矩陣 $\displaystyle A$ 的秩（Rank），即矩陣 $\displaystyle A$ 中線性獨立行或列的最大數目，同時也是奇異值矩陣 $\displaystyle \Sigma$ 中非零奇異值的數量，表示著矩陣 $\displaystyle A$ 中所包含的獨立資訊。

另一方面， $\displaystyle r$ 同時也影響了分解後 $\displaystyle U$ 、 $\displaystyle \Sigma$ 、 $\displaystyle V^T$ 矩陣的有效範圍。一般來說，當 $r < n$ 並且 $r < m$ 時，我們可以通過去除 $\displaystyle U$ 和 $\displaystyle V^T$ 中的某些行列來得到更小的分解結果，節省儲存空間。此類方法在像是 PCA 等資料壓縮（降維）的方法中非常常見。

如何計算 SVD

要計算 SVD，可以遵循以下步驟：

計算 $\displaystyle A^{T}A$ 和 $\displaystyle AA^{T}$
求解 $\displaystyle V$ 和 $\displaystyle \Sigma$
求解 $\displaystyle U$
組合 $\displaystyle U$ 、 $\displaystyle \Sigma$ 、 $\displaystyle V^T$

在過程中，我也會透過 Python 一步步進行驗算。

假設我們有以下矩陣 $\displaystyle A$ ：

$\displaystyle A = \begin{bmatrix} 3 & 2 \\ 2 & 3 \\ 1 & 1 \end{bmatrix}$

而我們嘗試將其做 SVD 分解。

1. 計算 $\displaystyle A^{T}A$ 和 $\displaystyle AA^{T}$

$\displaystyle A^T = \begin{bmatrix} 3 & 2 & 1 \\ 2 & 3 & 1 \end{bmatrix}$

接著計算 $\displaystyle A^T$ $\displaystyle A$ 和 $\displaystyle A$ $\displaystyle A^T$ ：

$\displaystyle A^T A = \begin{bmatrix} 3 & 2 & 1 \\ 2 & 3 & 1 \end{bmatrix} \times \begin{bmatrix} 3 & 2 \\ 2 & 3 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} 14 & 13 \\ 13 & 14 \end{bmatrix}$

$\displaystyle AA^T = \begin{bmatrix} 3 & 2 \\ 2 & 3 \\ 1 & 1 \end{bmatrix} \times \begin{bmatrix} 3 & 2 & 1 \\ 2 & 3 & 1 \end{bmatrix} = \begin{bmatrix} 13 & 12 & 5 \\ 12 & 13 & 5 \\ 5 & 5 & 2 \end{bmatrix}$

接著透過 Python 進行驗算：

import numpy as np

A = np.array(
    [
        [3, 2],
        [2, 3],
        [1, 1],
    ],
)

# A^T A
At_A = np.dot(A.T, A)
print("A^T A =\n", At_A)

print("\n")

# A A^T
A_At = np.dot(A, A.T)
print("A A^T =\n", A_At)

Output:

A^T A =
 [[14 13]
 [13 14]]


A A^T =
 [[13 12  5]
 [12 13  5]
 [ 5  5  2]]

2. 求解 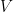$\displaystyle V$ 和 $\displaystyle \Sigma$

求解特徵值（Eigan）

首先，我們通過對矩陣 $\displaystyle A^{T}A$ 進行特徵值分解來求解矩陣 $\displaystyle V$ 和奇異值矩陣 $\displaystyle \Sigma$ 。

特徵值的計算 $\displaystyle \lambda$ 滿足以下特徵方程：

$\displaystyle det(A^{T}A-\lambda I) = 0$

所以我們可以計算出一個可供求解 $\displaystyle \lambda$ 的公式：

$\displaystyle A^T A - \lambda I = \begin{bmatrix} 14-\lambda & 13 \\ 13 & 14-\lambda \end{bmatrix}$

$\displaystyle \text{det}\left(\begin{bmatrix} 14-\lambda & 13 \\ 13 & 14-\lambda \end{bmatrix}\right) = (14-\lambda)(14-\lambda) - 13 \times 13=0$

$\displaystyle \lambda^2 - 28\lambda + 27 = 0$

最後透過公式解，我們可以得到：

$\displaystyle \lambda_1 = 27, \quad \lambda_2 = 1$

求解奇異值

而特徵值的平方根即為奇異值，之後可用來建構 $\displaystyle \Sigma$ 矩陣：

$\displaystyle \sigma_1 = \sqrt{\lambda_1} = \sqrt{27} = 5.196, \quad \sigma_2 = \sqrt{\lambda_2} = 1$

所以 $\displaystyle \Sigma$ 矩陣為：

$\displaystyle \Sigma = \begin{bmatrix} 5.196 & 0 \\ 0 & 1 \end{bmatrix}$

求解特徵向量

接著我們可以透過以下方程式求解特徵向量 $\displaystyle v$ ：

$\displaystyle (A^{T}A-\lambda I)v = 0$

當 $\displaystyle \lambda = 27$ 時：

$\displaystyle \begin{bmatrix} 14-27 & 13 \\ 13 & 14-27 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} -13 & 13 \\ 13 & -13 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = 0$

得到：

$\displaystyle v_1=v_2$

將其做正規化，特徵向量為：

$\displaystyle v_1 = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0.7071 \\ 0.7071 \end{bmatrix}$

當 $\displaystyle \lambda = 1$ 時：

$\displaystyle \begin{bmatrix} 14-1 & 13 \\ 13 & 14-1 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} 13 & 13 \\ 13 & 13 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = 0$

$\displaystyle -v_1=v_2$

同樣將其做正規化：

$\displaystyle v_2 = \frac{1}{\sqrt{2}} \begin{bmatrix} -1 \\ 1 \end{bmatrix} = \begin{bmatrix} -0.7071 \\ 0.7071 \end{bmatrix}$

最後我們可以得到 $\displaystyle V$ 為：

$\displaystyle V = \begin{bmatrix} v_1 & v_2 \end{bmatrix} = \begin{bmatrix} 0.7071 & -0.7071 \\ 0.7071 & 0.7071 \end{bmatrix}$

接著我們同樣透過 Python 驗證：

# Calculate eigenvalues and eigenvectors of `A^T A`
eigvals_AtA, eigvecs_AtA = np.linalg.eig(At_A)

# Caculate singular values
singular_values = np.sqrt(eigvals_AtA)

# Arrange eigenvalues and corresponding eigenvectors in descending order (make sure they are consistent with np.svd)
idx = eigvals_AtA.argsort()[::-1]
eigvals_AtA = eigvals_AtA[idx]
eigvecs_AtA = eigvecs_AtA[:, idx]


print("The Eigenvalues of `A^T A`:\n", eigvals_AtA)
print("\n")

print("The Eigenvectors of `A^T A` (V):\n", V)
print("\n")

print("Singular Values (Σ):\n", singular_values)

Output:

The Eiganvalues of `A^T A`:
[27. 1.]

The Eiganvectors of `A^T A` (V):
[[ 0.70710678 -0.70710678]
 [ 0.70710678 0.70710678]] 

Singular Values (Σ):
[5.19615242 1. ]

3. 求解 $\displaystyle U$

求解 $\displaystyle U$ 和前面的步驟基本上完全一樣，不過由於 $\displaystyle U$ 的尺寸比較大，所以計算上比較麻煩一點。在這裡，我就由程式幫我計算，偷攋一下。

eigvals_AAt, eigvecs_AAt = np.linalg.eig(A_At)

print("The Eigenvalues of `A A^T`:\n", eigvals_AAt)
print("\n")

print("The Eigenvectors of `A A^T` (U):\n", eigvecs_AAt)

Output:

The Eigenvalues of `A A^T`:
[ 2.70000000e+01 1.00000000e+00 -1.33858608e-16]

The Eigenvectors of `A A^T` (U):
[[ 6.80413817e-01 7.07106781e-01 -1.92450090e-01]
 [ 6.80413817e-01 -7.07106781e-01 -1.92450090e-01]
 [ 2.72165527e-01 2.07171358e-16 9.62250449e-01]]

Step 4. 組合 $\displaystyle U$ 、 $\displaystyle \Sigma$ 、 $\displaystyle V^T$

在我們開始把 $\displaystyle U$ 、 $\displaystyle \Sigma$ 、 $\displaystyle V^T$ 組合起來之前，我們需要確保 $\displaystyle U$ 和 $\displaystyle V$ 的方向一致，這是 SVD 分解中的一個重要步驟。

這是因為在計算特徵向量時，特徵向量的方向是任意的。也就是說，如果 $\displaystyle v$ 是一個特徵向量、那麼 $\displaystyle -v$ 也會同樣是一個特徵向量。

# Get (m, n)
m, n = A.shape
min_dim = min(m, n)

# Get Σ
Sigma = np.zeros((m, n))
Sigma[:min_dim, :min_dim] = np.diag(singular_values)

# Get U, V
U = eigvecs_AAt
V = eigvecs_AtA

# Check the direction
for i in range(min_dim):
    if np.dot(A, V[:, i])[0] * U[0, i] < 0:
        U[:, i] = -U[:, i]

# Reconstruction
A_reconstructed = np.dot(np.dot(U, Sigma), V.T)
print("A_reconstructed:\n", A_reconstructed)

Output:

A_reconstructed:
[[3. 2.]
 [2. 3.]
 [1. 1.]]

結語

本文簡單地探討了奇異值分解（SVD）的實現過程與步驟，闡述了如何計算 $U$ , $\Sigma$ , $V$ 等矩陣，並特別關注了 U 和 V 方向一致性的重要性。

這個過程不僅展示了 SVD 的數學原理，也揭示了在實際計算時需要考慮的細節。

理解 SVD 的這些細節對於我們在實際應用中正確使用這一強大工具非常關鍵。現在無論是在資料壓縮、降維、圖像處理還是推薦系統等各種不同的領域，深入理解 SVD 的工作原理都能幫助我們更好地應用和優化相關算法。

尤其像我做 AI 方面相關的研究，越是想要減少儲存空間，大家就越常探討 SVD 的應用；SVD 的重要性可見一斑。

References

機率密度函數 (Probability Density Function, PDF)

[Machine Learning] 旋轉位置嵌入（Rotary Position Embedding, RoPE）筆記

奇異值分解（Singular Value Decomposition, SVD）筆記

如何計算 SVD

1. 計算 $\displaystyle A^{T}A$ 和 $\displaystyle AA^{T}$

2. 求解 $\displaystyle V$ 和 $\displaystyle \Sigma$

求解特徵值（Eigan）

求解奇異值

求解特徵向量

3. 求解 $\displaystyle U$

Step 4. 組合 $\displaystyle U$ 、 $\displaystyle \Sigma$ 、 $\displaystyle V^T$

結語

References

Read More

相關

Leave a Reply取消回覆

奇異值分解（Singular Value Decomposition, SVD）筆記

如何計算 SVD

1. 計算 和

2. 求解 和

求解特徵值（Eigan）

求解奇異值

求解特徵向量

3. 求解

Step 4. 組合 、、

結語

References

Read More

分享此文：

相關

Leave a Reply取消回覆

1. 計算 $\displaystyle A^{T}A$ 和 $\displaystyle AA^{T}$

2. 求解 $\displaystyle V$ 和 $\displaystyle \Sigma$

3. 求解 $\displaystyle U$

Step 4. 組合 $\displaystyle U$ 、 $\displaystyle \Sigma$ 、 $\displaystyle V^T$