Skip to content

Note Of Singular Value Decomposition (SVD)

Last Updated on 2024-08-11 by Clay

Singular Value Decomposition (SVD) is a method for decomposing a matrix into three matrices, revealing the rank, data dimensions, and key directions of the original matrix. It is often used in dimensionality reduction, compression, and structural analysis.

Let A be a matrix of size m \times n. The SVD can be written as:

\displaystyle A = U \Sigma V^T

Here, U has dimensions m \times m, \Sigma has dimensions m \times n, and V^T has dimensions n \times n. Additionally:

  • U is an orthogonal matrix, meaning U^T = U^{-1}, and represents the left singular vectors of A.
  • V is also an orthogonal matrix, meaning V^T = V^{-1}, and represents the right singular vectors of A.
  • \Sigma is a diagonal matrix (though not necessarily square), with non-zero values only on the diagonal. These diagonal values are the singular values of A.

In the figure above, r represents the rank of the matrix A, which is the maximum number of linearly independent rows or columns in A. It also corresponds to the number of non-zero singular values in the \Sigma matrix, indicating the independent information contained within A.

On the other hand, r also influences the effective range of the decomposed matrices U, \Sigma, and V^T. Generally, when r < n and r < m, we can reduce the size of the decomposed matrices by removing certain rows or columns from U and V^T, thereby saving storage space. This approach is common in data compression methods, such as PCA.

How to Compute SVD

To compute SVD, follow these steps:

  1. Compute A^{T}A and AA^{T}
  2. Solve for V and \Sigma
  3. Solve for U
  4. Assemble U, \Sigma, V^T

Along the way, I’ll verify the calculations using Python.

Let’s assume we have the following matrix A:

\displaystyle A = \begin{bmatrix} 3 & 2 \\ 2 & 3 \\ 1 & 1 \end{bmatrix}

We will attempt to decompose it using SVD.


1. Compute A^{T}A and AA^{T}

A^T = \begin{bmatrix} 3 & 2 & 1 \\ 2 & 3 & 1 \end{bmatrix}

Next, we calculate A^T A and A A^T:

A^T A = \begin{bmatrix} 3 & 2 & 1 \\ 2 & 3 & 1 \end{bmatrix} \times \begin{bmatrix} 3 & 2 \\ 2 & 3 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} 14 & 13 \\ 13 & 14 \end{bmatrix}

AA^T = \begin{bmatrix} 3 & 2 \\ 2 & 3 \\ 1 & 1 \end{bmatrix} \times \begin{bmatrix} 3 & 2 & 1 \\ 2 & 3 & 1 \end{bmatrix} = \begin{bmatrix} 13 & 12 & 5 \\ 12 & 13 & 5 \\ 5 & 5 & 2 \end{bmatrix}

Let’s verify these calculations using Python:

import numpy as np

A = np.array(
    [
        [3, 2],
        [2, 3],
        [1, 1],
    ],
)

# A^T A
At_A = np.dot(A.T, A)
print("A^T A =\n", At_A)

print("\n")

# A A^T
A_At = np.dot(A, A.T)
print("A A^T =\n", A_At)


Output:

A^T A =
 [[14 13]
 [13 14]]


A A^T =
 [[13 12  5]
 [12 13  5]
 [ 5  5  2]]



2. Solve for 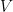V and \Sigma

Compute Eigenvalues

First, we solve for matrix V and the singular value matrix \Sigma by performing eigenvalue decomposition on the matrix A^{T}A.

The eigenvalues \lambda satisfy the following characteristic equation:

\text{det}(A^{T}A-\lambda I) = 0

We can then compute the equation for solving \lambda:

A^T A - \lambda I = \begin{bmatrix} 14-\lambda & 13 \\ 13 & 14-\lambda \end{bmatrix}

\text{det}\left(\begin{bmatrix} 14-\lambda & 13 \\ 13 & 14-\lambda \end{bmatrix}\right) = (14-\lambda)(14-\lambda) - 13 \times 13=0

\lambda^2 - 28\lambda + 27 = 0

Finally, solving the equation gives:

\lambda_1 = 27, \quad \lambda_2 = 1


Compute Singular Values

The singular values are the square roots of the eigenvalues, which we use to construct the \Sigma matrix:

\sigma_1 = \sqrt{\lambda_1} = \sqrt{27} = 5.196, \quad \sigma_2 = \sqrt{\lambda_2} = 1

So the \Sigma matrix is:

\Sigma = \begin{bmatrix} 5.196 & 0 \\ 0 & 1 \end{bmatrix}


Compute Eigenvectors

Next, we can solve for the eigenvectors v using the following equation:

(A^{T}A-\lambda I)v = 0

When \lambda = 27:

\begin{bmatrix} 14-27 & 13 \\ 13 & 14-27 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} -13 & 13 \\ 13 & -13 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = 0

This gives:

v_1=v_2

After normalization, the eigenvector is:

v_1 = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 0.7071 \\ 0.7071 \end{bmatrix}

When \lambda = 1:

\begin{bmatrix} 14-1 & 13 \\ 13 & 14-1 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} 13 & 13 \\ 13 & 13 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = 0

-v_1=v_2

Similarly, after normalization:

v_2 = \frac{1}{\sqrt{2}} \begin{bmatrix} -1 \\ 1 \end{bmatrix} = \begin{bmatrix} -0.7071 \\ 0.7071 \end{bmatrix}

Finally, we obtain V as:

V = \begin{bmatrix} v_1 & v_2 \end{bmatrix} = \begin{bmatrix} 0.7071 & -0.7071 \\ 0.7071 & 0.7071 \end{bmatrix}

Let’s verify this using Python:

# Calculate eigenvalues and eigenvectors of `A^T A`
eigvals_AtA, eigvecs_AtA = np.linalg.eig(At_A)

# Caculate singular values
singular_values = np.sqrt(eigvals_AtA)

# Arrange eigenvalues ​​and corresponding eigenvectors in descending order (make sure they are consistent with np.svd)
idx = eigvals_AtA.argsort()[::-1]
eigvals_AtA = eigvals_AtA[idx]
eigvecs_AtA = eigvecs_AtA[:, idx]


print("The Eigenvalues of `A^T A`:\n", eigvals_AtA)
print("\n")

print("The Eigenvectors of `A^T A` (V):\n", V)
print("\n")

print("Singular Values (Ξ£):\n", singular_values)


Output:

The Eigenvalues of `A^T A`:
[27. 1.]

The Eigenvectors of `A^T A` (V):
[[ 0.70710678 -0.70710678]
 [ 0.70710678 0.70710678]] 

Singular Values (Ξ£):
[5.19615242 1. ]



3. Solve for 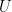U

Solving for U follows essentially the same steps as before. However, since the dimensions of U are larger, the calculations are a bit more involved. Here, I’ll let the code do the heavy lifting for me.

eigvals_AAt, eigvecs_AAt = np.linalg.eig(A_At)

print("The Eigenvalues of `A A^T`:\n", eigvals_AAt)
print("\n")

print("The Eigenvectors of `A A^T` (U):\n", eigvecs_AAt)


Output:

The Eigenvalues of `A A^T`:
[ 2.70000000e+01 1.00000000e+00 -1.33858608e-16]

The Eigenvectors of `A A^T` (U):
[[ 6.80413817e-01 7.07106781e-01 -1.92450090e-01]
 [ 6.80413817e-01 -7.07106781e-01 -1.92450090e-01]
 [ 2.72165527e-01 2.07171358e-16 9.62250449e-01]]



Step 4. Assemble 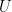U, \Sigma, V^T

Before we start assembling U, \Sigma, and V^T, we need to ensure that the directions of U and V are consistent. This is an important step in the SVD decomposition process.

This is because when calculating eigenvectors, the direction of the eigenvector is arbitrary. In other words, if v is an eigenvector, then -v is also an eigenvector.

# Get (m, n)
m, n = A.shape
min_dim = min(m, n)

# Get Ξ£
Sigma = np.zeros((m, n))
Sigma[:min_dim, :min_dim] = np.diag(singular_values)

# Get U, V
U = eigvecs_AAt
V = eigvecs_AtA

# Check the direction
for i in range(min_dim):
    if np.dot(A, V[:, i])[0] * U[0, i] < 0:
        U[:, i] = -U[:, i]

# Reconstruction
A_reconstructed = np.dot(np.dot(U, Sigma), V.T)
print("A_reconstructed:\n", A_reconstructed)


Output:

A_reconstructed:
[[3. 2.]
 [2. 3.]
 [1. 1.]]

Conclusion

This article briefly discusses the process of Singular Value Decomposition (SVD), explaining how to compute U, \Sigma, and V matrices, with a focus on the importance of ensuring directional consistency between U and V.

This process not only demonstrates the mathematical principles behind SVD but also highlights the practical considerations during computation.

Understanding these details is crucial for correctly using this powerful tool in practice. Whether in data compression, dimensionality reduction, image processing, or recommendation systems, a deep understanding of SVD’s working principles can help us better apply and optimize related algorithms.

In AI-related research, the more we seek to reduce storage space, the more often we explore the applications of SVD. The importance of SVD cannot be overstated.

References

Read More

What Is Probability Density Function (PDF)?

Tags:

Leave a Reply